Debby Cintia Antika/21212753
Dinda Tamara Putri/22212189
Feby Dharma Pratiwi/22212880
Indina Tarziah/23212683
Maytias Tri Pratiwi/24212505
1 EB 18
Konsep Nilai Waktu Uang
Setiap keluarga baik bapak maupun ibu pasti mengusahakan agar kehidupan keuangan keluarganya berjalan dengan aman dan tentram, terbebas dari berbagai masalah. Bekerja dari pagi sampai petang dilakoninya dengan sabar agar semua kebutuhan serta keinginannya tercapai. Dengan pendapatan bulanan yang diterima tentunya setiap keluarga harus mengalokasikan untuk berbagai kebutuhan keluarga, baik jangka pendek maupun jangka. Setiap harinya kita selalu dihadapi oleh pilihan-pilihan seputar keuangan; BELANJA atau MENABUNG, BELI atau JUAL. Keputusan ini terlihat adalah keputusan saat itu, tapi keputusan yang Anda ambil sekarang akan berdampak dalam jangka panjang.
¡ Uang yang diterima sekarang nilainya lebih besar daripada uang yang diterima di masa mendatang.
¡ Lebih awal uang anda menghasilkan bunga, lebih cepat bunga tersebut menghasilkan bunga.
1. Nilai Yang Akan Datang
Nilai yang akan datang adalah nilai uang dimasa yang akan datang dari uang yang diterima atau dibayarkan pada masa sekarang dengan memperhitungkan tingkat bunga setiap periode.
Nilai masa depan uang yang anda tabung atau investasikan hari ini akan tergantung pada:
a. Besarnya dana yang anda tabungkan
b. Tingkat suku bunga atau return dari tabungan anda
c. Lamanya dana tersebut akan ditabungkan
FVn = PV(1 + i)n
d. FV = Nilai mendatang dari investasi pada akhir tahun ke-n
e. I = tingkat bunga tahunan
f. PV = nilai sekarang dari sejumlah uang yang diinvestasikan
Contoh :
PV = Rp 2.000.000
i = 10% n = 5 tahun
FV5 = 2000000 x (1+0.1)5
= 2000000 x 1.61051
= 3221020
Jadi, nilai uang pada 5 tahun kedepan adalah sebesar Rp. 3.221.020,-
Persamaan ini dipergunakan untuk menghitung nilai dari sebuah investasi pada titik waktu di masa mendatang.
2. Nilai Sekarang
Nilai sekarang adalah nilai sejumlah uang yang saat ini dapat dibungakan untuk memperoleh jumlah yang lebih besar dimasa mendatang.
¡ Tingkat bunga diskonto (the discount rate) atau bunga yang dipergunakan untuk menghitung nilai sekarang dari nilai yang ditetapkan dimasa mendatang.
¡ Present-value interest factor (PVIFi,n) adalah nilai digunakan untuk menghitung nilai Persamaan awal
FVn = PV(1 + i)n
a) PV = FVn (1/ (1 + i)n
b) PV = FVn (PVIFi,n)
c) PV = nilai sekarang dari sejumlah uang di masa mendatang
d) FVn = nilai investasi pada akhir tahun ke-n
e) PVIFi,n = the present value interest factor
Persamaan ini digunakan untuk menentukan berapa nilai sekarang dari sejumlah uang dimasa mendatang.
Contoh :
1. Jika dijanjikan mendapat uang sebesar $500,000 pada waktu 40 tahun mendatang, dengan asumsi bunga 6%, berapa nilai sekarang dari uang yang dijanjikan?
PV = FVn (PVIFi,n)
PV = $500,000 (PVIF6%, 40 yr)
PV = $500,000 (.097)
PV = $48,500
Jadi, nilai sekarang dari uang sebesar $500,000 yang dijanjikan pada waktu 40 tahun kemudian bernilai $48,500.
2. Setahun lagi rudi akan menerima uang sebanyak Rp. 10.000,-. Berapakah nilai sekarang uang tersebut jika tingkat bunga adalah 13 % setahun?
Dalam masalah ini:
A = 10.000,-. r = 0,13 dan t = 1
P = 10.000/ 1 + (0,13)(1)= 8849,56
3. Nilai Masa Datang Dan Nilai Sekarang
· Nilai masa datang adalah nilai uang dimasa yang akan datang dari uang yang diterima atau dibayarkan pada masa sekarang dengan memperhitungkan tingkat bunga setiap periode.
· Nilai sekarang adalah nilai sejumlah uang yang saat ini dapat dibungakan untuk memperoleh jumlah yang lebih besar dimasa mendatang.
Pada point 1 – 3 terdapat istilah-istilah sebagai berikut :
Pv = Present Value (Nilai Sekarang)
Fv = Future Value (Nilai yang akan datang)
I = Bunga (i = interest / suku bunga)
n = tahun ke-n
An = Anuity atau anuitas
SI = Simple interest dalam rupiah
P0 = pokok/jumlah uang yg dipinjam/dipinjamkan pada periode waktu
4. Annuitas
Pengertian
Anuitas adalah serangkaian pembayaran yang sama untuk jumlah tahun tertentu.
Anuitas dibagi menjadi dua tipe dasar:
1) Anuitas biasa, yaitu anuitas dengan pembayaran di akhir periode
2) Anuitas jatuh tempo, yaitu anuitas dengan pembayaran pada awal periode
Dalam anuitas, terdapat juga angsuran dan bunga.
Angsuran adalah suatu pembayaran dengan jumlah tertentu, yang mungkin jumlahnya dapat berbeda dan waktu dapat tidak teratur. Tetapi pada anuitas jumlah pembayaran sama dan jangka waktu juga sama.
Besar anuitas adalah besarnya angsuran ditambah dengan bunga yang diperhitungkan.
Karakteristik Anuitas :
1) Jumlah yang dibayarkan tiap periodenya sama
2) Jangka waktunya sama
3) Suku bunga yang diberlakukan tertentu
Rumus umum anuitas :
Misal :
Pak Thomas tiap bulan membayar kredit rumahnya yang terdiri dari angsuran sebesar
Rp. 300.000,00 dan bunga sebesar Rp. 125.000,00, maka:
Rp. 300.000,00 dan bunga sebesar Rp. 125.000,00, maka:
anuitas yang dibayarkan adalah Rp. 425.000,00 (Rp.300.000,00 + Rp. 125.000,00).
Artinya:
anuitas kredit rumah yang harus dibayar Pak Thomas tiap bulan sebesar Rp. 425.000,00.
Artinya:
anuitas kredit rumah yang harus dibayar Pak Thomas tiap bulan sebesar Rp. 425.000,00.
Contoh anuitas : premi asuransi jiwa, pembayaran hadiah lotre, pembayaran dana pensiun, dan lain sebagainya.
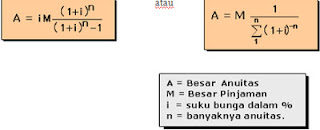
Untuk menentukan besarnya anuitas digunakan pula rumus sebagai berikut :
Contoh :
Josima meminjam uang dari Bank BRI sebesar Rp. 10.000.000,00, pembayaran dilakukan dengan cara anuitas dengan memperhitungkan bunga 2% per bulan. Pinjaman lunas selama 3 tahun dengan pembayaran bulanan. Berapa jumlah pembayaran (anuitas) yang harus dibayar Josima tiap bulan?
Penyelesaian :
Diketahui: M = Rp. 10.000.000,00
i = 2% per bulan
n = 3 tahun = 36 bulan
Rumus :
Jadi, besarnya Anuitas adalah sebesar Rp. 329.328,53
Anuitas dan Pembulatan
Bila diperhatikan perhitungan anuitas sebelumnya nilai rupiah kurang realistis, karena hasilnya lebih dari dua angka dibelakang koma, sedangkan kenyataannya pembayaran dalam pecahan rupiah pun sulit dilakukan. Oleh karena itu agar hasilnya lebih realistis dilakukan pembulatan. Pembulatan dapat dilakukan dalam puluhan rupiah, ratusan rupiah atau ribuan rupiah baik keatas maupun kebawah.
Misal nilai anuitas sebesar Rp. 16,461,721.82 dibulatkan sebagai berikut :
Dalam puluhan rupiah menjadi Rp. 16.461.720,00
Dalam ratusan rupiah menjadi Rp. 16.461.700,00
Dalam ribuan rupiah menjadi Rp. 16.462.000,00
Akibat pembulatan tersebut akan terjadi kelebihan atau kekurangan pembayaran. Kelebihan atau kekurangan ini diperhitungkan pada pembayaran anuitas terakhir.
Jadi besarnya Anuitas adalah sebesar Rp. 392.328,53
Contoh :
Andra meminjam uang sebesar Rp. 50.000.000,00 pinjaman itu akan dilunasi dengan cara anuitas selama 2 tahun yang pembayarannya setiap 6 bulan. Bunga yang ditetapkan 24% per tahun. Hitunglah besarnya Anuitas dan buatlah tabel rencana angsuran !
Penyelesaian :
Diketahui:
|
M = Rp. 50.000.000,00
i = 24% per tahun = 12% per 6 bulan (semester)
n = 2 tahun = 4 semester
A = 16.461.761,82
Atau menggunakan table rencana angsuran.
| |
Menentukan Angsuran Periode Tertentu
Keterangan :
an = Angsuran periode tertentu atau ke n
A = Anuitas
M = Jumlah uang yang dipinjam
i = Suku bunga
n = Periode tertentu atau ke n
i = Suku bunga
n = Periode tertentu atau ke n
Atau menggunakan table rencana angsuran.
Menentukan Sisa Utang Periode Tertentu
Keterangan :
a1 = Angsuran periode ke 1 = A - Mi
A = Anuitas
M = Jumlah uang yang dipinjam
i = Suku bunga
n = Periode tertentu atau ke n
Dengan tabel :
|
Menentukan Bunga pada Periode tertentu
Keterangan :
a1 = Angsuran periode ke 1 = A - Mi
A = Anuitas M = Jumlah uang yang dipinjam i = Suku bunga n = Periode tertentu atau ke n |
4.1 Anuitas Biasa
Anuitas biasa atau Ordinary annuity adalah sebuah anuitas yang diperhitungkan pada setiap akhir interval seperti akhir bulan, akhir kuartal , akhir setiap 6 bulan, maupun pada setiap akhir tahun.
Rumus dasar future value anuitas biasa adalah sebagai berikut :
FVn = PMT1 + in - 1 i
Keterangan :
FVn = Future value ( nilai masa depan dari anuitas pada akhir tahun ke - n )
PMT = Payment ( pembayaran anuitas yang disimpan atau diterima pada setiap periode )
i = Interest rate ( tingkat bunga atau diskonto tahunan )
n = Jumlah tahun akan berlangsungnya anuitas
Rumus dasar present value anuitas biasa adalah sebagai berikut :
PVn = FVn1 - 1 ( 1 + i ) n i
PVn = Present value ( nilai sekarang dari anuitas pada akhir tahun ke - n )
4.2 Anuitas Terhutang
Anuitas terhutang adalah anuitas yang pembayarannya dilakukan pada setiap awal interval. Awal interval pertama merupakan perhitungan bunga yang pertama dan awal interval kedua merupakan perhitungan bunga kedua dan seterusnya.
Rumus dasar future value anuitas terhutang adalah :
FVn = PMT ( FVIFAi,n ) ( 1 + i )
Rumus dasar present value anuitas terhutang adalah :
PVn = PMT ( PVIFAi,n ) ( 1 + i )
4.3 Nilai Sekarang Anuitas
Nilai sekarang anuitas adalah nilai hari ini dari pembayaran sejumlah dana tertentu yang dilakukan secara teratur selama waktu yang telah ditentukan.Perhitungan nilai sekarang anuitas juga akan memberikan hasil yang berbeda jika anda melakukan investasi pada awal atau akhir tahun , dimana rumus perhitungannya adalah
Jika dilakukan pada awal tahun , menjadi :
PV anuitas = nilai investasi x Faktor PV x ( 1 + r )
Jika dilakukan pada akhir tahun , menjadi :
PV anuitas = nilai investasi x Faktor PV
PV anuitas = nilai investasi x Faktor PV x ( 1 + r )
Jika dilakukan pada akhir tahun , menjadi :
PV anuitas = nilai investasi x Faktor PV
4.4 Nilai Sekarang Dari Anuitas Terhutang
Nilai sekarang dari anuitas terhutang berguna untuk mengukur setiap pembayaran yang maju satu periode atau pembayaran pada awal tahun dengan menggunakan formulasi :
An (Anuitas Terhutang) = PMT ( PVIFA (r,n ) ( 1 + r )
4.5 Anuitas abadi
Anuitas abadi adalah serangkaian pembayaran yang sama jumlahnya dan diharapkan akan berlangsung terus menerus.
PV ( anuitas abadi ) = pembayaran / Tingkat suku bunga = PMT / i
4.6 Nilai Sekarang Dan Seri Pembayaran Yang Tidak Rata
Persamaan umum berikut ini bisa digunakan untuk mencari nilai sekarang dari seri pembayaran yang tak rata. Nilai sekarang anuitas abadi = PMTt adalah pembayaran ditahun t.
Sehingga menjadi : PV= PMTt(PVIFr,t)
4.7 Periode Kemajemukan Tengah Tahunan Atau Periode Lainnya
Bunga majemuk tahunan adalah proses aritmatika untuk menentukan nilai akhir dari arus kas atau serangkaian arus kas apabila suku bunga ditambahkan satu kali dalam setahun. Sedangkan bunga majemuk setengah tahunan adalah proses aritmatika untuk menentukan nilai akhir dari arus kas atau serangkaian arus kas apabila suku bunga ditambahkan dua kali dalam setahun.
4.8 Amortisasi Pinjaman
Salah satu penerapan penting dari bunga majemuk adalah pinjaman yang dibayarkan secara dicicil selama waktu tertentu. Termasuk didalamnya adalah kredit mobil , kredit kepemilikan rumah , kredit pendidikan , dan pinjaman - pinjaman bisnis lainnya selain pinjaman jangka waktu sangat pendek dan obligasi jangka panjang. Jika suatu pinjaman akan dibayarkan dalam periode yang sama panjangnya ( bulanan , kuartalan , atau tahunan ) , maka pinjaman ini disebut juga sebagai pinjaman yang diamortisasi.
Sumber :
·
M.
Fuad, Christine H. Pengantar Bisnis . Jakarta: PT.
Gramedia Pustaka Utama